Dirac delta function

The Dirac delta function, often written as $\delta (x)$, is a made-up concept by mathematician Paul Dirac. It is a really pointy and skinny function that pokes out a point along a wave. Loosely speaking, it has the value of zero everywhere except at $x=0$, in such a way that the area between the function and the x-axis adds up to 1. The delta function is often used in sampling theory, where its pointiness is useful for getting clean samples.

Schematic representation of the Dirac delta function by a line surmounted by an arrow. The height of the arrow is usually used to specify the value of any multiplicative constant, which will give the area under the function. The other convention is to write the area next to the arrowhead.

The Dirac delta function as the limit (in the sense of distributions) of the sequence of zero-centered normal distributions $\delta _{a}(x)={\frac {1}{a{\sqrt {\pi }}}}\mathrm {e} ^{-x^{2}/a^{2}}$ as $a\rightarrow 0$.

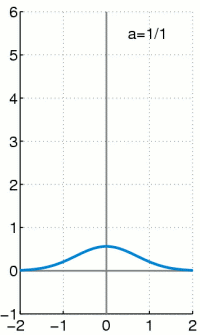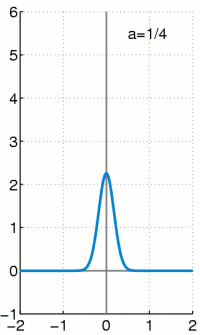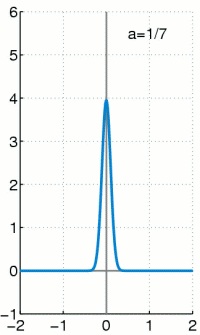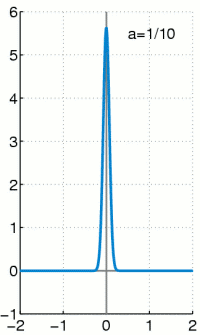
The integral of the Dirac delta function is the Heaviside function. The Dirac delta function can be seen as the derivative of the Heaviside function.

Related pages

• Special functions