Fibonacci number

The Fibonacci numbers are a sequence of numbers in mathematics named after Leonardo of Pisa, known as Fibonacci. Fibonacci wrote a book in 1202, called Liber Abaci ("Book of Calculation"), which introduced the number pattern to Western European mathematics, although mathematicians in India already knew about it.^[1]^[2]

The first number of the pattern is 0, the second number is 1, and each number after that is equal to adding the two numbers right before it together. For example 0+1=1 and 3+5=8. This sequence goes on forever.

F₀	F₁	F₂	F₃	F₄	F₅	F₆	F₇	F₈	F₉	F₁₀	F₁₁	F₁₂	F₁₃	F₁₄	F₁₅	F₁₆	F₁₇	F₁₈	F₁₉	F₂₀
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765

This can be written as a recurrence relation,

F_{n}=F_{n-1}+F_{n-2}

For this to make sense, at least two starting points need to be given. Here, $F_{0}=0$ and $F_{1}=1$ .

Fibonacci numbers in nature

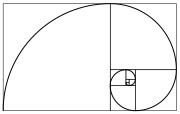
Sunflower head displaying florets in spirals of 34 and 55 around the outside

Fibonacci numbers are related to the golden ratio, which shows up in many places in buildings and in nature.^[3] Some examples are the pattern of leaves on a stem, the parts of a pineapple,^[4] the flowering of artichoke, the uncurling of a fern and the arrangement of a pine cone.^[5] The Fibonacci numbers are also found in the family tree of honeybees.^[6]^[7]

Binet's Formula

The nth Fibonacci number can be written in terms of the golden ratio. This avoids having to use recursion to calculate Fibonacci numbers, which can take a computer a long time to do.

F_{n}={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}

Where $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ , the golden ratio.

References

↑ Parmanand Singh. "Acharya Hemachandra and the (so called) Fibonacci Numbers". Math. Ed. Siwan, 20(1):28-30, 1986. ISSN 0047-6269
↑ Parmanand Singh,"The So-called Fibonacci numbers in ancient and medieval India." Historia Mathematica 12(3), 229–44, 1985.
↑ S. Douady and Y. Couder (1996). "Phyllotaxis as a Dynamical Self Organizing Process" (PDF). Journal of Theoretical Biology. 178 (3): 255–274. doi:10.1006/jtbi.1996.0026. Archived from the original (PDF) on 2006-05-26. Retrieved 2008-08-01.
↑ Jones, Judy; William Wilson (2006). "Science". An Incomplete Education. Ballantine Books. p. 544. ISBN 978-0-7394-7582-9.
↑ A. Brousseau (1969). "Fibonacci Statistics in Conifers". Fibonacci Quarterly (7): 525–532.
↑ "Computer Science for Fun - cs4fn: Marks for the da Vinci Code: B-". www.cs4fn.org.
↑ Scott, T.C.; Marketos, P. (March 2014), On the Origin of the Fibonacci Sequence (PDF), MacTutor History of Mathematics archive, University of St Andrews

Other websites

[1] Parmanand Singh. "Acharya Hemachandra and the (so called) Fibonacci Numbers". Math. Ed. Siwan, 20(1):28-30, 1986. ISSN 0047-6269

[2] Parmanand Singh,"The So-called Fibonacci numbers in ancient and medieval India." Historia Mathematica 12(3), 229–44, 1985.

[3] S. Douady and Y. Couder (1996). "Phyllotaxis as a Dynamical Self Organizing Process" (PDF). Journal of Theoretical Biology. 178 (3): 255–274. doi:10.1006/jtbi.1996.0026. Archived from the original (PDF) on 2006-05-26. Retrieved 2008-08-01.

[4] Jones, Judy; William Wilson (2006). "Science". An Incomplete Education. Ballantine Books. p. 544. ISBN 978-0-7394-7582-9.

[5] A. Brousseau (1969). "Fibonacci Statistics in Conifers". Fibonacci Quarterly (7): 525–532.

[6] "Computer Science for Fun - cs4fn: Marks for the da Vinci Code: B-". www.cs4fn.org.

[7] Scott, T.C.; Marketos, P. (March 2014), On the Origin of the Fibonacci Sequence (PDF), MacTutor History of Mathematics archive, University of St Andrews

[1]

[2]

[3]

[4]

[5]

[6]

[7]