Finite element method

The finite element method is a numerical method of solving systems of differential equations.^[1]^[2] They are used extensively in many fields of engineering because they require very little knowledge of mathematics beyond basic algebra to use.^[1]^[2] It belongs to the Methods of Weighted residuals.^[3] The problem is formulated such that some conditions are satisfied exactly, while others are satisfied only approximately or numerically (i.e., the "residual" being the difference between the exact solution and the approximate solution is weighted and minimized to get the best approximation).

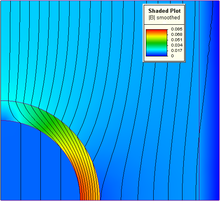
While the ease of setting up a problem using finite elements and getting a solution is the reason for its popularity, it is also the cause of its frequent misuse and distrust of the answers obtained.^[4] Usually you have to check your results with an experiment before your model is acceptable for use. The use of finite elements in structural analysis is in particular poorly managed. Engineers typically begin working with FEM having very little knowledge of numerical methods or knowledge of finite element behavior. There are no standards and guidelines for modeling and few managers who understand well enough to regulate modeling. It has led to mistrust of the method, its arrested development, and some very bad analysis being performed that is copied by others. Much aircraft structural design is analyzed using FEM.

References

↑ ^1.0 ^1.1 Brenner, S., & Scott, R. (2007). The mathematical theory of finite element methods (Vol. 15). Springer Science & Business Media.
↑ ^2.0 ^2.1 Oden, J. T., & Reddy, J. N. (2012). An introduction to the mathematical theory of finite elements. Courier Corporation.
↑ Finlayson, B. A., & Scriven, L. E. (1966). The method of weighted residuals—a review. Appl. Mech. Rev, 19(9), 735-748.
↑ Babuska, I., Strouboulis, T., & Babuška, I. (2001). The finite element method and its reliability. Oxford University Press.

Related pages

This short article about mathematics can be made longer. You can help Wikipedia by adding to it.

[bs-1] 1.0 ^1.1 Brenner, S., & Scott, R. (2007). The mathematical theory of finite element methods (Vol. 15). Springer Science & Business Media.

[or-2] 2.0 ^2.1 Oden, J. T., & Reddy, J. N. (2012). An introduction to the mathematical theory of finite elements. Courier Corporation.

[3] Finlayson, B. A., & Scriven, L. E. (1966). The method of weighted residuals—a review. Appl. Mech. Rev, 19(9), 735-748.

[4] Babuska, I., Strouboulis, T., & Babuška, I. (2001). The finite element method and its reliability. Oxford University Press.

[1]

[2]

[3]

[4]