Limit of a sequence

For the general mathematical concept, see Limit (mathematics).

In mathematics, a sequence is an ordered set of mathematical objects (most notably a list of numbers). In some cases, the sequence tends towards a limit, in which case the limit is denoted using the symbol $\lim$ (as in $\lim _{n\to \infty }a_{n}$), and the sequence is said to be convergent, otherwise it is divergent.

The plot of a convergent sequence {a_n} is shown in blue. Visually we can see that the sequence is converging to the limit 0 as n increases.

The plot of a Cauchy sequence (x_n), shown in blue, as x_n versus n. Visually, we see that the sequence appears to be converging to a limit point as the terms in the sequence become closer together as n increases. In the real numbers every Cauchy sequence converges to some limit.

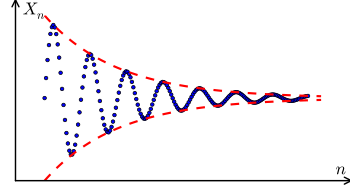
In a convergent sequence, the absolute difference between the value of the current term and the limit, $|x_{n}-\lim(X)|$, will decrease towards 0, as the sequence progresses.

Formal Definition

We call $x$ the limit of the sequence $(x_{n})$ if the following condition holds:

• For each real number $\epsilon >0$, there exists a natural number $N$ such that, for every natural number $n>N$, we have $|x_{n}-x|<\epsilon$.

In other words, for every measure of distance $\epsilon$, we can find an infinite number of terms of the sequence that are closer than $\epsilon$ to the limit. We say that the sequence $(x_{n})$ converges to or tends to the limit $x$, which we write as $x_{n}\to x$ or $\lim _{n\to \infty }x_{n}=x$. The limit can be also shown to be unique.

If a sequence converges to a limit, then it is convergent; otherwise it is divergent.

History

The Greek philosopher Zeno of Elea is famous for formulating paradoxes that involve limiting processes.

Leucippus, Democritus, Antiphon, Eudoxus and Archimedes developed the method of exhaustion, which uses an infinite sequence of approximations to determine an area or a volume. Archimedes succeeded in summing what is now called a geometric series.

Newton dealt with series in his works on Analysis with infinite series (written in 1669, circulated in manuscript, published in 1711), Method of fluxions and infinite series (written in 1671, published in English translation in 1736, Latin original published much later) and Tractatus de Quadratura Curvarum (written in 1693, published in 1704 as an Appendix to his Optiks). In the latter work, Newton considers the binomial expansion of (x+o)ⁿ, which he then linearizes by taking the limits as o tends to 0.

In the 18th century, mathematicians like Euler succeeded in summing some divergent series by stopping at the right moment; they did not much care whether a limit existed, as long as it could be calculated. At the end of the century, Lagrange in his Théorie des fonctions analytiques (1797) opined that the lack of rigour precluded further development in calculus. Gauss in his etude of hypergeometric series (1813) for the first time rigorously investigated under which conditions a series converged to a limit.

The modern definition of a limit (for any ε there exists an index N so that ...) was given by Bernhard Bolzano (Der binomische Lehrsatz, Prague 1816, little noticed at the time), and by Karl Weierstraß in the 1870s.

Related pages

• Limit of a function