Quadratic equation

A quadratic equation is an equation where its highest exponent is 2 (which is why it is called 'quadratic' from the Latin word quadratus 'square'). These equations can be rearranged to the standard form which is^[1]ː

$ax^{2}+bx+c=0$

where a is not equal to 0, otherwise the equation is linear.

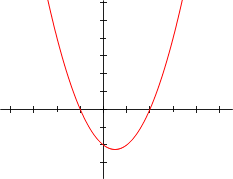
It makes a parabola (a "U" shape) when graphed on a coordinate plane. When people work with quadratic equations, one of the most common things they do is to solve it. This means to find the points on a coordinate grid where the graphed equation crosses the x-axis, or the horizontal axis. These points are called the "zeroes", or "roots", of a function. In other words, to solve the equation means to find the value of x so that $ax^{2}+bx+c=0$ , where the coefficients, a, b, and c, are all real numbers. There are different ways to find out the value of x. Plotting the function on a graph is one way. In the picture on the right, the function crosses the x-axis at the points $(-1,0)$ and $(2,0)$ .

Graphing a quadratic equation makes it is very easy to find the roots, but it is not always convenient. So there are different ways to do this using math.

Solving quadratic equations

A quadratic equation with real or complex coefficients has two solutions, called roots. These two solutions may or may not be equal, and they may or may not be a real number.

Factoring

Some quadratic equations, like $2x^{2}-x-1=0$ , can be factorized. This equation can be written as $(2x+1)(x-1)=0$ , which produces two separate equations, $2x+1=0$ and $x-1=0$ . This is because when any of the two equations is equal to zero, the original equation is equal to zero because the two equations are multiplied together to form the quadratic equation. From this equation, it is easy to use algebra to find out what the value of x is. In the first of the two equations, $x=-1/2$ and in the second, $x=1$ . This means that these two values of x will make the whole quadratic equation equal to zero. The y-coordinate is equal to zero at these values of x, and so the coordinates $(-1/2,0)$ and $(1,0)$ are the places where the graph of the function crosses the x-axis.^[2]

Completing the square

Not all quadratic equations can be factorized, such as $5x^{2}-4x-2=0$ . One of the ways to solve these kinds of equations is called completing the square. This means to find some value for "k" below so that: $x^{2}+{\frac {b}{a}}x+k=x^{2}+2xy+y^{2},\,\!$ for some y. Since $y={\frac {b}{2a}}\,\!$ and $k=y^{2},\,\!$ this means $k={\frac {b^{2}}{4a^{2}}}.\,\!$

There are five steps to solve a quadratic equation by completing the square:

Divide the equation by the value of a (here, a is equal to 5): $x^{2}-{\frac {4}{5}}x-{\frac {2}{5}}=0$
Move the number term (the one without any coefficients, here ${\frac {2}{5}}$ ) to the other side: $x^{2}-{\frac {4}{5}}x={\frac {2}{5}}$
Complete the square by adding $k={\frac {b^{2}}{4a^{2}}}$ to both sides on the equation, as was described above. This value here is $k={\frac {16}{100}}={\frac {4}{25}}$ . This gives $x^{2}-{\frac {4}{5}}x+{\frac {4}{25}}={\frac {10}{25}}+{\frac {4}{25}}$ , and the left side can be factored to give $\left(x-{\frac {2}{5}}\right)^{2}={\frac {14}{25}}$
Find the square root of both sides. The $\pm$ is there since the square root is for both positive and negative values: $x-{\frac {2}{5}}=\pm {\sqrt {\frac {14}{25}}}$
Finally, move the number term to the other side to get a value for x: $x=\pm {\sqrt {\frac {14}{25}}}+{\frac {2}{5}}$

This last value for x has two values: $x={\sqrt {\frac {14}{25}}}+{\frac {2}{5}}\approx 1.148$ and $x=-{\sqrt {\frac {14}{25}}}+{\frac {2}{5}}\approx -0.348$ . These are the x-coordinates at the points where the y-coordinates are equal to zero and so the function crosses the x-axis.

It is also interesting to note that the vertex of the function, $\left({\frac {2}{5}},-{\frac {14}{25}}\right)$ , can be found from the equation in step 3 above.^[3]

The quadratic formula

quadratic equation in graph

Although completing the square can be used to solve many quadratic equations, it does not work with every equation. There is a way to find the value of x that makes the equation true by replacing the values in a formula with the coefficients from the quadratic equation. This is called the "quadratic formula", which is:

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}

The numbers represented by a, b, and c are the same as those in the original equation, $ax^{2}+bx+c=0$ . For this formula to work properly, a cannot be equal to 0 for the formula (but really, when a = 0 in the original equation, it is not quadratic since there is no x-squared term).

The factored form of this equation is $y=a(x-s)(x-t)$ , where s and t are the zeros, a is a constant, and y and the two values of x are ordered pairs which satisfy the equation.^[4]

Proof of the formula

The quadratic formula can be found out, or proved, using the same completing the square method from above, only by using a, b, and c instead of actual values and using algebra to find the value of x. Here is how:

Divide the equation by a: $x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0$
Move ${\frac {c}{a}}$ to the other side: $x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}$
Complete the square by adding $k={\frac {b^{2}}{4a^{2}}}$ to both sides on the equation, which gives: $x^{2}+{\frac {b}{a}}x+{\frac {b^{2}}{4a^{2}}}=-{\frac {c}{a}}+{\frac {b^{2}}{4a^{2}}}.\,\!$ The left side is now a perfect square; it is the square of $x+{\frac {b}{2a}}.\,\!$ The right side can be a single fraction, with a common denominator $4a^{2}$ : $\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}$
Find the square root of both sides: $x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}$
Finally, move ${\frac {b}{2a}}$ to the other side: $x=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}$ ^[5]

Using the quadratic formula

Now that the value of x has been found out, the values of a, b, and c are replaced with the corresponding coefficients from the original equation. For example, going back to the second example, $5x^{2}-4x-2=0$ , it can be seen that the values are $a=5$ , $b=-4$ , and $c=-2$ . By putting these values into the quadratic formula and solving, the result is:

$x={\frac {-(-4)\pm {\sqrt {(-4)^{2}-4(5)(-2)}}}{2(5)}}={\frac {4\pm {\sqrt {56}}}{10}}$ . Solving the two square roots, the value of x can be either 1.148 or -0.348, which is the same as above.

Unlike the other methods described above, the quadratic equation will work with every possible value for a, b, and c, even if there are no "real roots", that is, places where the graph of the function touches the x-axis.

The value inside the square root, that is, $b^{2}-4ac$ , is known as the discriminant. It can tell whether the roots are real or Imaginary. There are three cases:

If the discriminant is positive, there will be two values for x and therefore two separate roots, one at each place where the graph crosses the x-axis.
If the discriminant is equal to zero, there is only one value for x, but there are in fact two roots which are equal. The graph touches the x-axis at its vertex, but does not cross it.
If the discriminant is negative, there is no real value of x. On a graph, the function does not even touch the x-axis, but the roots are still there. The value of the roots here is a complex number, which uses the value i to represent ${\sqrt {-1}}$ .^[6]

History

Babylonian mathematicians, as early as 2000 BC (displayed on Old Babylonian clay tablets) could solve problems relating the areas and sides of rectangles. There is evidence dating this algorithm as far back as the Third Dynasty of Ur.^[7] In modern notation, the problems typically involved solving a pair of simultaneous equations of the form:

x+y=p,\ \ xy=q,

which is equivalent to the statement that $x$ and $y$ are the roots of the equation:^[8]^: 86

z^{2}+q=pz.

The steps given by Babylonian scribes for solving the above rectangle problem, in terms of $x$ and $y$ , were as follows:

Compute half of p.
Square the result.
Subtract q.
Find the (positive) square root using a table of squares.
Add together the results of steps (1) and (4) to give $x$ .

In modern notation this means calculating $x=\left({\frac {p}{2}}\right)+{\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}$ , which is equivalent to the modern day quadratic formula for the larger real root (if any) $x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}$ with $a=1$ , $b=-p$ , and $c=q$ .