Subset
set whose elements are all contained in another set
In set theory, a set is called a subset of a set if all of the elements of are contained in . For example, any set is a subset of itself. Another example of a subset is a proper subset: a set is called a proper subset of a set if is subset of but is not equal to .
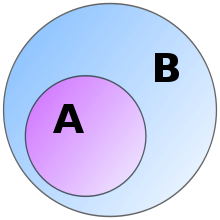
The symbol "" always means "is a subset of."[1][2][3] The symbol "" always means "is a proper subset of." There is also the symbol "", which some authors use to mean "is a subset of"[4] and other authors only use to mean "is a proper subset of."[1]
For example:
- is a subset of , so we could write .
- is a proper subset of , so we could write ,, or .
- The interval [0, 1] is a proper subset of the set of real numbers , so .
Related pages
changeReferences
change- ↑ 1.0 1.1 "Comprehensive List of Set Theory Symbols". Math Vault. 2020-04-11. Retrieved 2020-08-23.
- ↑ Weisstein, Eric W. "Subset". mathworld.wolfram.com. Retrieved 2020-08-23.
- ↑ "Introduction to Sets". www.mathsisfun.com. Retrieved 2020-08-23.
- ↑ Rudin, Walter (1987), Real and complex analysis (3rd ed.), New York: McGraw-Hill, p. 6, ISBN 978-0-07-054234-1, MR 0924157












![{\displaystyle [0,1]\subset \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/98ef6fb8c5d9b34f4ba677930a956bd62270f9a2)