Octahedron

An octahedron is a polyhedron made of eight faces. In the case of the regular octahedron, these faces are triangles. The octahedron looks like two pyramids, which share the same base.

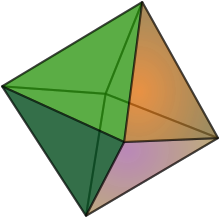
Dice: The one in the middle is an Octahedron.

In chemistry, octahedra are common: diamonds and fluorite are examples of crystals that are octahedra.

Regular octahedron

Dimensions

If the edge length of a regular octahedron is a, the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is

r_{u}={\frac {a}{2}}{\sqrt {2}}\approx 0.707\cdot a

and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is

r_{i}={\frac {a}{6}}{\sqrt {6}}\approx 0.408\cdot a

while the midradius, which touches the middle of each edge, is

r_{m}={\frac {a}{2}}=0.5\cdot a

Orthogonal projections

The octahedron has four special orthogonal projections, centered, on an edge, vertex, face, and normal to a face. The second and third correspond to the B₂ and A₂ Coxeter planes.

Orthogonal projections
Centered by	Edge	Face Normal	Vertex	Face
Image
Projective symmetry	[2]	[2]	[4]	[6]

Spherical tiling

The octahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Orthographic projection	Stereographic projection

Cartesian coordinates

An octahedron with edge length √2 can be placed with its center at the origin and its vertices on the coordinate axes; the Cartesian coordinates of the vertices are then

( ±1, 0, 0 );

( 0, ±1, 0 );

( 0, 0, ±1 ).

In an x–y–z Cartesian coordinate system, the octahedron with center coordinates (a, b, c) and radius r is the set of all points (x, y, z) such that

\left|x-a\right|+\left|y-b\right|+\left|z-c\right|=r.

Area and volume

The surface area A and the volume V of a regular octahedron of edge length a are:

A=2{\sqrt {3}}a^{2}\approx 3.464a^{2}

V={\frac {1}{3}}{\sqrt {2}}a^{3}\approx 0.471a^{3}

Thus the volume is four times that of a regular tetrahedron with the same edge length, while the surface area is twice (because we have 8 rather than 4 triangles).

If an octahedron has been stretched so that it obeys the equation

\left|{\frac {x}{x_{m}}}\right|+\left|{\frac {y}{y_{m}}}\right|+\left|{\frac {z}{z_{m}}}\right|=1,

the formulas for the surface area and volume expand to become

A=4\,x_{m}\,y_{m}\,z_{m}\times {\sqrt {{\frac {1}{x_{m}^{2}}}+{\frac {1}{y_{m}^{2}}}+{\frac {1}{z_{m}^{2}}}}},

V={\frac {4}{3}}\,x_{m}\,y_{m}\,z_{m}.

Additionally the inertia tensor of the stretched octahedron is

I={\begin{bmatrix}{\frac {1}{10}}m(y_{m}^{2}+z_{m}^{2})&0&0\\0&{\frac {1}{10}}m(x_{m}^{2}+z_{m}^{2})&0\\0&0&{\frac {1}{10}}m(x_{m}^{2}-y_{m}^{2})\end{bmatrix}}.

These reduce to the equations for the regular octahedron when

x_{m}=y_{m}=z_{m}=a\,{\frac {\sqrt {2}}{2}}.

Geometric relations

The octahedron represents the central intersection of two tetrahedra

The interior of the compound of two dual tetrahedra is an octahedron, and this compound, called the stella octangula, is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron relate to the other Platonic solids. One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of an icosahedron. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly partitioning each edge into the golden mean along the direction of its vector. There are five octahedra that define any given icosahedron in this fashion, and together they define a regular compound.

Octahedra and tetrahedra can be alternated to form a vertex, edge, and face-uniform tessellation of space, called the octet truss by Buckminster Fuller. This is the only such tiling save the regular tessellation of cubes, and is one of the 28 convex uniform honeycombs. Another is a tessellation of octahedra and cuboctahedra.

The octahedron is unique among the Platonic solids in having an even number of faces meeting at each vertex. Consequently, it is the only member of that group to possess mirror planes that do not pass through any of the faces.

Using the standard nomenclature for Johnson solids, an octahedron would be called a square bipyramid. Truncation of two opposite vertices results in a square bifrustum.

The octahedron is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the pentagonal dipyramid, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.^[1]

Uniform colorings and symmetry

There are 3 uniform colorings of the octahedron, named by the triangular face colors going around each vertex: 1212, 1112, 1111.

The octahedron's symmetry group is O_h, of order 48, the three dimensional hyperoctahedral group. This group's subgroups include D_3d (order 12), the symmetry group of a triangular antiprism; D_4h (order 16), the symmetry group of a square bipyramid; and T_d (order 24), the symmetry group of a rectified tetrahedron. These symmetries can be emphasized by different colorings of the faces.

Name	Octahedron	Rectified tetrahedron (Tetratetrahedron)	Triangular antiprism	Square bipyramid	Rhombic fusil
Image (Face coloring)	(1111)	(1212)	(1112)	(1111)	(1111)
Coxeter diagram		=
Schläfli symbol	{3,4}	r{3,3}	s{2,6} sr{2,3}	ft{2,4} { } + {4}	ftr{2,2} { } + { } + { }
Wythoff symbol	4 \| 3 2	2 \| 4 3	2 \| 6 2 \| 2 3 2
Symmetry	O_h, [4,3], (*432)	T_d, [3,3], (*332)	D_3d, [2⁺,6], (2*3) D₃, [2,3]⁺, (322)	D_4h, [2,4], (*422)	D_2h, [2,2], (*222)
Order	48	24	12 6	16	8

Nets

It has eleven arrangements of nets.

Dual

The octahedron is the dual polyhedron to the cube.

Faceting

The uniform tetrahemihexahedron is a tetrahedral symmetry faceting of the regular octahedron, sharing edge and vertex arrangement. It has four of the triangular faces, and 3 central squares.

Octahedron	Tetrahemihexahedron

Related pages

Truncated octahedron

References

↑ Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010). "On well-covered triangulations. III". Discrete Applied Mathematics. 158 (8): 894–912. doi:10.1016/j.dam.2009.08.002. MR 2602814.

Other websites

"Octahedron" . Encyclopædia Britannica. Vol. 19 (11th ed.). 1911.
Eric W. Weisstein, Octahedron at MathWorld.
Editable printable net of an octahedron with interactive 3D view
Paper model of the octahedron
K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
The Uniform Polyhedra
Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Conway Notation for Polyhedra Try: dP4

This short article about mathematics can be made longer. You can help Wikipedia by adding to it.

[1] Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010). "On well-covered triangulations. III". Discrete Applied Mathematics. 158 (8): 894–912. doi:10.1016/j.dam.2009.08.002. MR 2602814.

[1]