Riemann sum
In mathematics, the Riemann sum is a method of approximating the integral of a function over an interval. One representation of the integral, is the area under a curve in a graph. The Riemann sum is calculated by splitting the region into equal parts. In each part, the function is replaced by a shape. Shapes that are commonly used are rectangles, trapezoids, parabolas and cubics.The area of the similar shape can then be calculated. This method is often used when finding the closed form integral is difficult or impossible. The shapes used also influence how accurate the approximation is. More complex shapes give a higher accuracy, but this also means that calculating the approximation becomes more difficult.
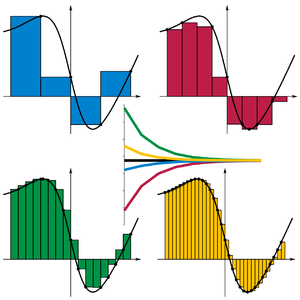
Because the region filled by the small shapes is usually not exactly the same shape as the region being measured, the Riemann sum will differ from the area being measured. This error can be reduced by dividing up the region more finely, using smaller and smaller shapes. As the shapes get smaller and smaller, the sum approaches the Riemann integral.
The Riemann sum may also be used to define the integration operation. The sum is named after a German mathematician who was called Bernhard Riemann.
Definition
changeYou divide the horizontal length under the part of the function you want to evaluate into "n" equal pieces. That is the n on top of the Σ (Greek letter sigma). The (xi-xi-1) represents the size of one horizontal segment that is created from dividing the whole by the "n". The f(yi) is a y value in an "n" segment. Since the area of a rectangle is length × width, the multiplication of xi and f(yi) is the area of a rectangle for that part of the graph. The Σ means we add up all of these small rectangles to get an approximation of the area under the segment of a function.