Tetradecagon

A tetradecagon or 14-gon is a shape with 14 sides and 14 corners.

Regular tetradecagon
A regular tetradecagon
Type	Regular polygon
Edges and vertices	14
Schläfli symbol	{14}, t{7}
Coxeter diagram
Symmetry group	Dihedral (D14), order 2×14
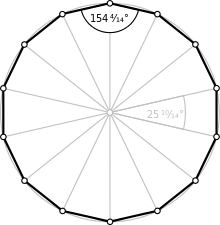
Internal angle (degrees)	≈154.2857°
Dual polygon	Self
Properties	Convex, cyclic, equilateral, isogonal, isotoxal

Regular tetradecagon

A regular tetradecagon has Schläfli symbol {14} and can be constructed as a quasiregular truncated heptagon, t{7}, which alternates two types of edges.

Area

The amount of space a regular tetradecagon takes up is

The area of a regular tetradecagon of side length a is given by

${\begin{aligned}A&={\frac {14}{4}}a^{2}\cot {\frac {\pi }{14}}={\frac {14}{4}}a^{2}\left({\frac {{\sqrt {7}}+4{\sqrt {7}}\cos \left({{\frac {2}{3}}\arctan {\frac {\sqrt {3}}{9}}}\right)}{3}}\right)\\&\simeq 15.3345a^{2}\end{aligned}}$

a is the length of one of its sides.

Dissection

Coxeter states that every parallel-sided 2m-gon can be divided into m(m-1)/2 rhombs. For the regular tetradecagon, m=7, and it can be divided into 21: 3 sets of 7 rhombs. This decomposition is based on a Petrie polygon projection of a 7-cube, with 21 of 672 faces. The list A006245 defines the number of solutions as 24698, including up to 14-fold rotations and chiral forms in reflection.

Dissection into 21 rhombs

Numismatic use

The regular tetradecagon is used as the shape of some commemorative gold and silver Malaysian coins, the number of sides representing the 14 states of the Malaysian Federation.

Other websites

• Eric W. Weisstein, Tetradecagon at MathWorld.