Molecular orbital

In chemistry, a molecular orbital (or MO) explains what happens to electrons when atoms join together in a molecule. A MO is a mathematical function which describes the wave-like behaviour of an electron in a molecule. The functions can tell the probability of finding an electron in any specific region. Chemists use such functions to predict or explain chemical and physical properties.

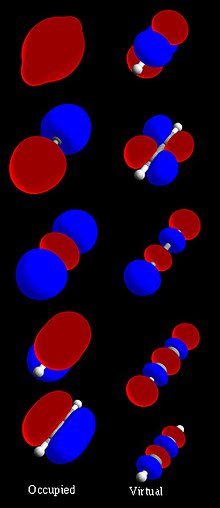
Chemists usually build mathematical models of molecular orbitals by combining atomic orbitals. Hybrid orbitals from each atom of the molecule, or other molecular orbitals from groups of atoms can also be used. Computers can work on these functions. Molecular orbitals allow chemists to apply quantum mechanics to study molecules. MOs answer questions about how the atoms in molecules stick together. The various rounded shapes in an orbital diagram indicate where electrons would most likely be found in an atom.

Figure 1: Complete acetylene (H–C≡C–H) molecular orbital set

History

The word orbital was first used in English by Robert S. Mulliken. The German physicist Erwin Schrödinger wrote about MOs earlier. Schrödinger called them Eigenfunktion.

Physicist Max Born described the theory behind molecular orbitals in 1926. Today, it is known as Born's rule and is part of the Copenhagen interpretation of quantum mechanics. When initially proposed, this theory did not agree with the atom model of Niels Bohr. Bohr's model described electrons as "orbiting" the nucleus, as they moved around in circles. However, the Born model eventually gained popular support because it was able to describe the locations of electrons within molecules and explained a number of previously inexplicable chemical reactions.

Overview

Atomic orbitals predict the position of an electron in an atom. Molecular orbitals are created when atomic orbitals are brought together. A molecular orbital can give information about the electron configuration of a molecule. The electron configuration is the most likely position, and the energy of one (or one pair of) electron(s). Mostly a MO is represented as a linear combination of atomic orbitals (the LCAO-MO method), especially in approximate use. This means that chemists assume the chance of an electron being at any point in the molecule is the sum of the probabilities of the electron being there based on the individual atomic orbitals. LCAO-MO is a simple model of bonding in molecules, and is important for studying molecular orbital theory.

Theoretical chemists use computers to calculate the MOs of different molecules (both real and imaginary). The computer can draw graphs of the "cloud" to show how likely the electron will be in any region. The computers can also give information about the physical properties of the molecule. They can also say how much energy is required to form the molecule. This helps chemists say whether some small molecules can be combined to make bigger molecules.

Most present-day ways of doing computational chemistry begin by calculating the MOs of a system. Each MO's electric field is generated by the nuclei of all the atoms and some average distribution of the other electrons.

Analogy

Calculating the MOs is like predicting the location of each employee in a home improvement store.

Understanding MOs is like the task of knowing where each employee is in a large home improvement store (without looking inside the store). An analyst knows the number of employees working at the store and each employee's department. He also knows that employees do not step on each other toes and employees stand in the aisle rather than on the merchandise shelves. Employees leave their own department to help customers locate merchandise in other departments or to check inventory. An analyst giving the location of all employees in the store at a selected moment without looking inside is like a chemist calculating the MOs of a molecule. Just as MOs cannot tell the exact location of each electron, the exact location of each employee is not known. An MO having a nodal plane is like the conclusion that employees walk down aisles and not through shelves. Although electrons are contributed from a specific atom, the electron fills an MO without regard to its source atom. This is like an employee leaving his department to walk elsewhere in the store during the day. So, an MO is an incomplete description of an electron just as the analyst's calculations about the unseen store is an incomplete guess about employee locations.

Formation of molecular orbitals

Theoretical chemists have invented rules for calculating MOs. These rules come from an understanding of quantum mechanics. Quantum mechanics helps chemists to use what physics said about electrons to work out how the electrons behave in molecules. Molecular orbitals form from "allowed" interactions between atomic orbitals. The interactions are "allowed" if the symmetries (determined from group theory) of the atomic orbitals are compatible with each other. Chemists study atomic orbital interactions. These interactions come from the overlap (a measure of how well two orbitals constructively interact with one another) between two atomic orbitals. The overlap is important if the atomic orbitals are close in energy. Finally, the number of MOs in a molecule must equal the number of atomic orbitals in the atoms being brought together to form the molecule.

Qualitative approach

Chemists need to understand the geometry of MOs in order to discuss molecular structure. The LCMO (Linear combination of atomic orbitals molecular orbital) method gives a rough but good description of the MOs. In this method, the molecular orbitals are expressed as linear combinations of all of the atomic orbitals of each atom in the molecule.

Linear combinations of atomic orbitals (LCAO)

Electron wavefunctions for the 1s orbital of the hydrogen atom (left and right) and the corresponding bonding (bottom) and antibonding (top) molecular orbitals of the H₂ molecule. The real part of the wavefunction is the blue curve, and the imaginary part is the red curve. The red dots mark the locations of the protons. The electron wavefunction oscillates according to the Schrödinger wave equation, and orbitals are its standing waves. The standing wave frequency is proportional to the orbital's energy. (This plot is a one-dimensional slice through the three-dimensional system.)

Molecular orbitals were first introduced by Friedrich Hund and Robert S. Mulliken in 1927 and 1928.

The linear combination of atomic orbitals or "LCAO" approximation for molecular orbitals was introduced in 1929 by Sir John Lennard-Jones. His ground-breaking paper showed how to derive the electronic structure of the fluorine and oxygen molecules from quantum principles. This qualitative approach to molecular orbital theory is part of the start of modern quantum chemistry.

Linear combinations of atomic orbitals can be used to guess the molecular orbitals that are made when the molecule’s atoms bond together. Similar to an atomic orbital, a Schrodinger equation, which describes the behavior of an electron, can be constructed for a molecular orbital as well. Linear combinations of atomic orbitals, (the sums and differences of the atomic wavefunctions) provide approximate solutions to the molecular Schrodinger equations. For simple diatomic molecules, the wavefunctions that you get are represented mathematically by the equations

Ψ = c_aψ_a + c_bψ_b

and

Ψ* = c_aψ_a - c_bψ_b

where Ψ and Ψ* are the molecular wavefunctions for the bonding and antibonding molecular orbitals, respectively, ψ_a and ψ_b are the atomic wavefunctions from atoms a and b, respectively, and c_a and c_b are adjustable coefficients. These coefficients can be positive or negative, depending on the energies and symmetries of the individual atomic orbitals. As the two atoms become closer together, their atomic orbitals overlap to produce areas of high electron density. So, molecular orbitals are formed between the two atoms. The atoms are held together by the electrostatic attraction between the positively charged nuclei and the negatively charged electrons occupying bonding molecular orbitals.

Bonding, Antibonding, and Nonbonding MOs

When atomic orbitals interact, the resulting molecular orbital can be of three types: bonding, antibonding, or nonbonding.

Bonding MOs:

• Bonding interactions between atomic orbitals are constructive (in-phase) interactions.
• Bonding MOs are lower in energy than the atomic orbitals that combine to produce them.

Antibonding MOs:

• Antibonding interactions between atomic orbitals are destructive (out-of-phase) interactions.
• Antibonding MOs are higher in energy than the atomic orbitals that combine to produce them.

Nonbonding MOs:

• Nonbonding MOs are the result of no interaction between atomic orbitals because of lack of compatible symmetries.
• Nonbonding MOs will have the same energy as the atomic orbitals of one of the atoms in the molecule.

HOMO and LUMO

See the main article: HOMO/LUMO

Each molecular orbital has its own energy level. Chemists sort the MOs by energy levels. Chemists assume that the electrons will fill the lowest energy level MOs first. For example, if a molecule has electrons to fill 15 orbitals, the 15 MOs with the lowest energy levels will be filled. The 15th MO on the list would be called the "highest occupied molecular orbital" (HOMO) and the 16th MO on the list would be the "lowest unoccupied molecular orbital" (LUMO). The difference in the HOMO's energy level and the LUMO's energy level is called the band gap. The band gap can sometimes serve as a measure of the excitability of the molecule: the smaller the energy, the more easily it will be excited. When the electron is excited, it will jump to an unoccupied MO. For example, this can help guess whether something will give out light (luminescence).

Other websites

• Java molecular orbital viewer shows orbitals of hydrogen molecular ion.
• The orbitron, a visualization of all atomic, and some molecular and hybrid orbitals
• xeo Visualizations of some atomic and molecular atoms
• Simulations of molecules with electrons caught in molecular orbital (Simulations run on PC only.)