Circle

A circle is a round, two-dimensional shape. All points on the edge of the circle are at the same distance from the center.

A Circle

The radius of a circle is a line from the center of the circle to a point on the side. Mathematicians use the letter $r$ for the length of a circle's radius. The center of a circle is the point in the very middle. It is often written as $O$.

The diameter (meaning "all the way across") of a circle is a straight line that goes from one side to the opposite and right through the center of the circle. Mathematicians use the letter $d$ for the length of this line. The diameter of a circle is equal to twice its radius ($d$ equals $2$ times $r$):

$d=2r$

The circumference (meaning "all the way around") of a circle is the line that goes around the center of the circle. Mathematicians use the letter $c$ for the length of this line.

The number $\pi$ (written as the Greek letter pi) is a very useful number. It is the length of the circumference divided by the length of the diameter ($\pi$ equals $c$ divided by $d$). As a fraction the number $\pi$ is equal to about ${\frac {22}{7}}$ or ${\frac {355}{113}}$ (which is closer) and as a number it is about $3.1415926536$.

	$\pi ={\frac {c}{d}}$
$\therefore {\textrm {(therefore)}}$	$c=2\pi r$
	$c=\pi d$

The area of the circle is equal to $\pi$ times the area of the gray square.

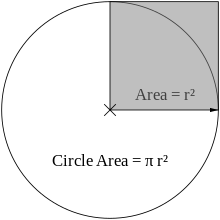
The area, $A$, inside a circle is equal to the radius multiplied by itself, then multiplied by $\pi$ ($A$ equals $\pi$ times $r$ times $r$).

$A=\pi r^{2}$

Calculating π

$\pi$ can be measured by drawing a circle, then measuring its diameter ($d$) and circumference ($c$). This is because the circumference of a circle is always equal to $\pi$ times its diameter.

$\pi ={\frac {c}{d}}$

$\pi$ can also be calculated by only using mathematical methods. Most methods used for calculating the value of $\pi$ have desirable mathematical properties. However, they are hard to understand without knowing trigonometry and calculus. However, some methods are quite simple, such as this form of the Gregory-Leibniz series:

$\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}+\cdots$

While that series is easy to write and calculate, it is not easy to see why it equals $\pi$. A much easier way to approach is to draw an imaginary circle of radius $r$ centered at the origin. Then any point $(x,y)$ whose distance $d$ from the origin is less than $r$, calculated by the Pythagorean theorem, will be inside the circle:

$d={\sqrt {x^{2}+y^{2}}}$

Finding a set of points inside the circle allows the circle's area $A$ to be estimated, for example, by using integer coordinates for a big $r$. Since the area $A$ of a circle is $\pi$ times the radius squared, $\pi$ can be approximated by using the following formula:

$\pi ={\frac {A}{r^{2}}}$

Calculating measures of a circle

Area

Using the radius: $A=\pi r^{2}={\frac {\tau r^{2}}{2}}$

Using the diameter: $A={\frac {\pi d^{2}}{4}}={\frac {\tau d^{2}}{8}}$

Using the circumference: $A={\frac {c^{2}}{2\tau }}={\frac {c^{2}}{4\pi }}$

Circumference

Using the radius: $c=\tau r=2\pi r$

Using the diameter: $c=\pi d={\frac {\tau d}{2}}$

Using the area: $c={\sqrt {2\tau A}}=2{\sqrt {\pi A}}$

Diameter

Using the radius: $d=2r$

Using the circumference: $d={\frac {c}{\pi }}={\frac {2c}{\tau }}$

Using the area: $d=2{\sqrt {\frac {A}{\pi }}}=2{\sqrt {\frac {2A}{\tau }}}$

Radius

Using the diameter: $r={\frac {d}{2}}$

Using the circumference: $r={\frac {c}{\tau }}={\frac {c}{2\pi }}$

Using the area: $r={\sqrt {\frac {A}{\pi }}}={\sqrt {\frac {2A}{\tau }}}$

Related pages

• Semicircle
• Sphere
• Squaring the circle
• Pi
• Tau

Other websites

• Calculate the measures of a circle online